|
Update: 2012/09/28
  
EDUCATION
Education Program
Undergraduate Program
The Department of Mathematics in the School of Science follows the same general educational policy of the Graduate School of Mathematics.
A. Educational Policy
The Department of Mathematics in the School of Science aims to cultivate self-motivated individuals, who can successfully navigate inquiry, reflection, and discovery based upon scholarly training in mathematics.
Our commitment is to establish an enlightening environment for problem-conscious students, where, together with sholars and fellow students, they can refine their ideas and apply logical reasoning in seeking solutions to problems.
Prospective students should know that in the mathematics department:
- Research planning, pursuit of research and regular reporting of results are expected.
- The education in the department is designed to support Students’ self-motivatation.
- Research is pursued in dialogue with active researchers and fellow students.
B. Study Hints to Remember
To ensure academic excellence, students are advised:
- To acquire an excellent command of and full appreciation of the fundamentals of mathematical knowledge.
- To familiarize themselves with various theoretical and conceptual aspects of different subject areas, and their broader meaning/applications.
C. Essential Abilities
Students are expected to develop the following research abilities:
- Learning skills, including advanced reading and literature search capabilities.
- Problem-solving skills involving the ability to analyze, reflect, synthesize and construct.
- Ability to apply assembled data and learned material to advance one’s research.
- Communication skills, including academic discussion, written expression and presentation.
D. Subjects to Learn
Students are expected to gain a strong command of the following through our curriculum:
- All areas of mathematics and mathematical science
- Ability to evaluate what is behind a given subject in the spectrum of mathematical genre
- Mathematical methodology and its approaches, such as systematic and logical ways of thinking
- Ways of defining positions and characteristics of mathematics in reference to the scientific method.
(While mathematical concepts may, at first glance, seem so abstract as to be irrelevant to social realtities, these concepts directly affect our natural surroundings and society.
The study of these phenomena is thus called mathematical science, and called mathematics when more universalized.)
The main features of our academic support systems are summarized below.
- Wide-ranging programs in a consistent and systematic curriculum for students’ various scholastic needs (ex. the Level System and Course Design enable students to choose their course works)
- Small group instruction at each level ensuring informed and effective teaching.
- Multiple advisory system for all undergraduate students above senior year, offering individual assistance with academic progress.
- Weekly office hours allowing students regular access to all faculty members.
The Level System is our central mechanism for classifying programs of study into educational purposes, organizing both undergraduate and graduate degree curriculums as a coherent whole.
Thus, all lectures and small group classes fall into a certain level.
- Level 0:
All science major students work together in the initial disciplinary phase of the art of science level 0 classes and learn subjects including calculus and linear algebra. - Level 1:
Level 1 classes deal with basic concepts, which all science-majored students need to comprehend.
This level corresponds to curricula for undergraduates in the second and third years.
These classes encourage students to apply and connect mathematical concepts with other fields of science, such as physics, and to develop intuitive, logical and abstract thinking. - Level 2:
The scope of level 2 classes embraces various areas of advanced concepts.
These classes provide scholarly training in logical, abstract and systematic approaches commonly used in mathematics through a wide diversity of subjects.
This level is intended for fourth year undergraduates and graduate students.
It is advisable to complete the set of classes within two years. - Level 3:
Level 3 classes serve as advanced courses, and are designed based upon the elemental portions of the curriculum up to level 2, the so-called core program.
These are intended for all 2nd year or above graduate students and should be completed over three or four years.
In this way students can pursue a purpose-centered education suited to their area of inquiry and unfettered by their official school year.
Level system and education program
In order to provide a comprehensive guide of course work, all instructors renew their Course Design each academic term, including the latest and detailed information about their courses.
Students are asked to refer to the course design for all information needed for course selection.
Students may find such entries as course title, instructor and contact information, course level, purpose and goal, contents and teaching style, course outline, textbooks and references, course prerequisites, grading scales, and study tips, etc.
For further information, please do not hesitate to contact the relevant course instructor.
C. Small Group Class
Small group instruction is offered for all school years.
- The 1st year to the first half of the 3rd year
Problem Exercise
Students apply knowledge learned in class to various mathematical exercises and in problem solving. - The rest of the 3rd year
Group Study
Students choose a subject and study it within groups. - The 4th year
Graduate Research
Students engage with lectures, presentations and discussions of a chosen subject actively and innovatively to develop their scholastic ability.
The graduate research class differentiates a course for advanced students in a seminar format involving student participation.
Small group classes offered in the Master’s program are also flexible in style.
D. Academic Advisor
An advisor is assigned to each student beyond the fourth year.
Your advisors will constantly meet, listen to, and advise you for your best academic performance, taking account of your progress and future career.
If necessary, the advisors let you acquaint yourselves with scholars and experts in specific fields.
We are proud of this advising system, by which more than one instructor serves as your guide for study.
- 1. Research toward graduation thesis (4th year students)
- is supported by a research instructor.
- 2. For the Master’ Program students
- Students may select a different advisor for the 1st year and for the 2nd year.
Or they may keep the same advisor through both the 1st and the 2nd years.
Moreover students may select another subadvisor who can provide an objective perspective on the student’s research and thesis organization.
- 3. Doctoral students
- Multiple advisors will be available but one member of faculty will act as main advisor.
- 0. Students transferring from other institutions
- There is an advising system particularly for those who are admitted to our department from other academic institutions.
Note: Advisors serve only as your guides.
Your own motivation is the key to your success.
E. Office Hours
Cafe David
All faculty members have weekly office hours during academic terms.
There is no need for prior appointments and you should feel free to visit instructors’ offices whenever you have questions or concerns.
There are mainly three types of office hours: regular office hours, office hours for specific courses, and joint office hours called Cafe David, which are held by teaching assistants.
The Core Curriculum was introduced in 2004 to align the contents of each course title so that the course content is consistent regardless of which faculty member teaches a course.
Now the core curriculum courses are defined, all students are assured of learning all necessary foundational knowledge.
The courses below are included in the core curriculum:
- Level 1:
- Foundations of Modern Mathematics A, B, C,
- Elements of Algebra,
- Elements of Geometry,
Elements of Analysis,
- Level 2:
- Sequel Course of Algebra,
- Sequel Course of Geometry,
- Sequel Course of Analysis.
The concept of the core curriculum and the information about corresponding courses can be found through the links below.
As the core curriculum defines only principles, the details of courses are up to each faculty member who takes charge of the course.
|
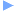Undergraduate Program
