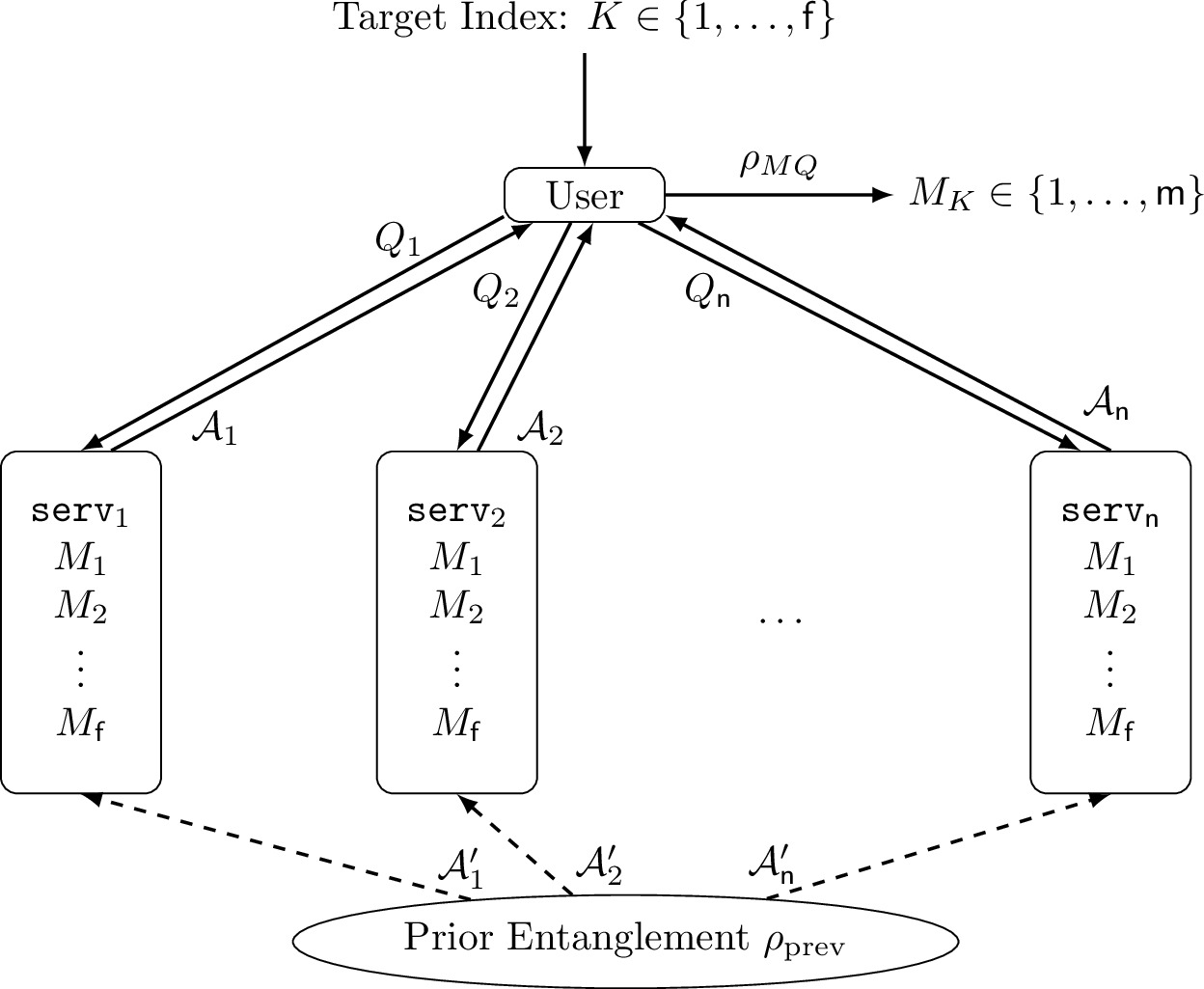
When a user retrieves information from databases, it is often required to protect the privacy of the user. Private information retrieval (PIR) is a protocol in which a user retrieves one of multiple messages from the server(s) without revealing which message is retrieved to any individual server. One simple solution for single-server PIR is to download all messages in the server, and this simple but inefficient solution is proved to be optimal for single-server PIR. To improve communication efficiency, multi-server PIR has been studied with the assumption that the servers cannot communicate with each other. Symmetric PIR is multi-server PIR with servers' secrecy in which the user only obtains the retrieved message but no other information of other messages.

1. Equivalence of Non-Perfect Secret Sharing and Symmetric Private Information Retrieval with General Access Structure
   by Seunghoan Song and Masahito Hayashi
   arXiv:2101.11194 [cs.CR], 2021.

   In this paper, we derive the equivalence relation between symmetric PIR, an extended class of PIR, and non-perfect secret sharing. By this relation, we prove a theoretic communication limit of symmetric PIR from that of non-perfect secret sharing.

1. Capacity of Quantum Private Information Retrieval with Multiple Servers
   by Seunghoan Song and Masahito Hayashi
   IEEE Transactions on Information Theory, 2020, in press.
   Presented at ISIT2019 (Talk), BeyondIID7 (Talk), AQIS2019 (Talk), QIP2020 (Poster).

   This paper derives the fundamental communication limit of symmetric and non-symmetric QPIR and constructs an optimal protocol achieving the communication limit. The optimal protocol is constructed only with two servers and achieves the same efficiency as retrieval without secrecy. This paper also proves that multi-round communication does not increase the communication efficiency of QPIR.

2. Capacity of Quantum Private Information Retrieval with Colluding Servers
   by Seunghoan Song and Masahito Hayashi
   Proceedings of 2020 IEEE International Symposium on Information Theory (ISIT), pp. 1727--1731, 2020.
   Presented at ISIT2020 (Talk), QCrypt2020 (Poster), BeyondIID8 (Lighting Talk), AQIS2020 (Talk).

   One critical weakness of multi-server QPIR is that the assumption of no communication among servers is too restrictive. t-Private QPIR is QPIR in which the identity of the retrieved message is kept secret even if at most t servers may communicate and collude. As an extension of [1], this paper derives the fundamental communication limit of symmetric and non-symmetric t-private QPIR and constructs an optimal protocol achieving the communication limit. The optimal protocol is constructed upon the quantum stabilizer formalism, and the optimality is proved by the classical-quantum channel coding capacity with prior entanglement.

3. Capacity of Quantum Private Information Retrieval with Collusion of All But One of Servers
   by Seunghoan Song and Masahito Hayashi
   Proceedings of 2019 IEEE Information Theory Workshop (ITW), pp. 1-5, 2019.
   Presented at ITW2019 (Talk), QIP2020 (Poster).

   This paper constructs an optimal symmetric QPIR protocol when all but one of the servers collude. The optimal protocol in this paper is designed constructively from quantum teleportation and superdense coding. Whereas the protocol in [2] is based on the quantum stabilizer formalism, which requires a multipartite entangled state, the protocol in this paper is constructed only with bipartite entangled states.

4. Quantum Private Information Retrieval for Quantum Messages
   by Seunghoan Song and Masahito Hayashi
   arXiv:2101.09041 [quant-ph], 2021.

   Even if there has been rigorous studies for QPIR for classical message retrieval, there has been no study for QPIR for quantum state retrieval. In this paper, we prove two results: 1) downloading all states in the server is the optimal solution for one-server QPIR for quantum states, and 2) there exists more efficient solution with multiple-server QPIR for quantum states.

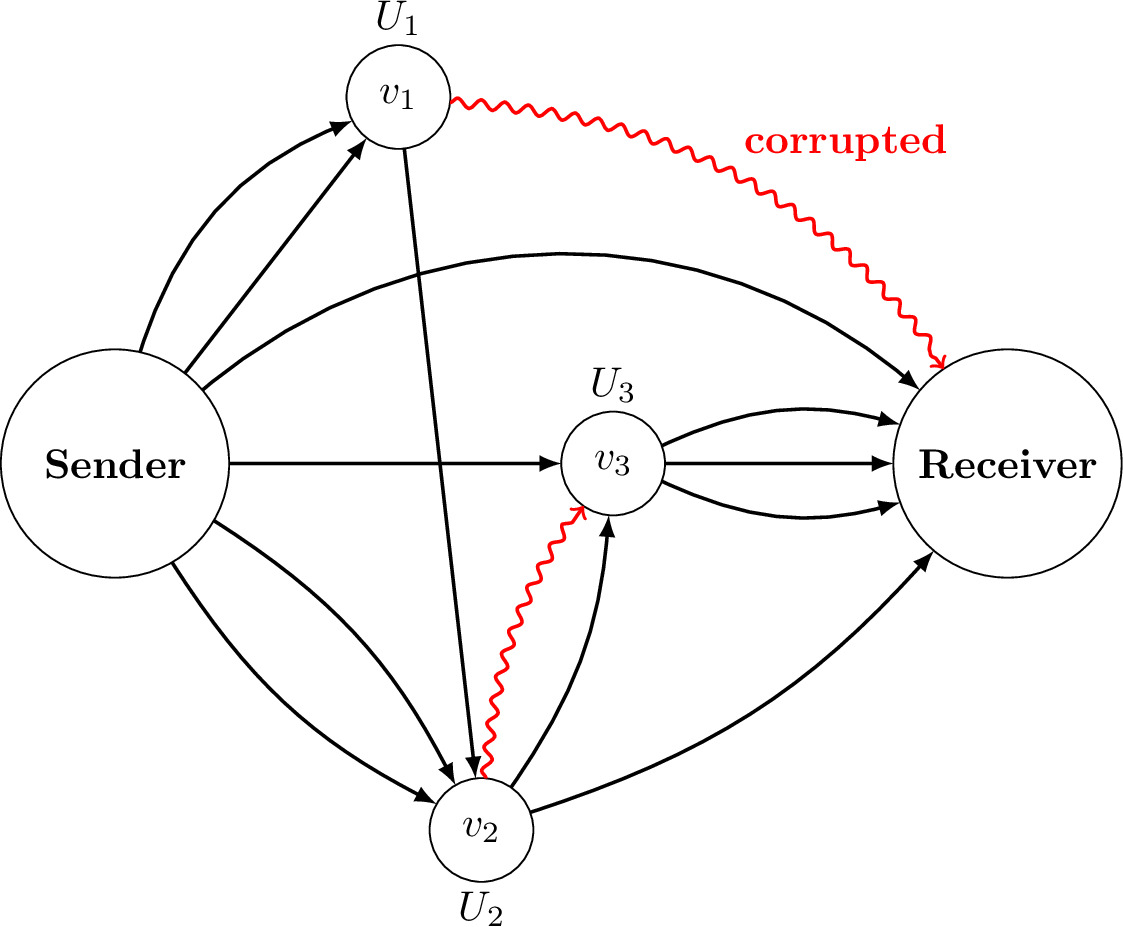
A quantum network is expected to be a basic infrastructure for quantum communication. A quantum network is composed of edges, which represent quantum communication channels to transmit quantum states, and nodes, which represent quantum processors to convert input quantum states to output quantum states. Since a quantum network connects a sender and a receiver by multiple paths, it enhances robust communication by diversification of risks when the network is eavesdropped and corrupted. Although the robust network communication against corruption has been discussed for classical networks, it has not been studied for quantum networks.

1. Secure Quantum Network Code without Classical Communication
   by Seunghoan Song and Masahito Hayashi
   IEEE Transactions on Information Theory, vol. 66, no. 2, pp. 1178-1192, 2020.
   Presented at ITW2018 (Talk), AQIS2018 (Poster).

   This paper constructs an end-to-end network code in which a sender can securely transmit a quantum state to a receiver when the malicious adversary corrupts edges whose number is less than half of the transmission rate. Our code is universal in the sense that the code is constructed without the knowledge of the specific node operations and the network topology. Our code can be thought of as a generalization of quantum-error correcting codes and quantum secret sharing.

2. Quantum Network Code for Multiple-Unicast Network with Quantum Invertible Linear Operation
   by Seunghoan Song and Masahito Hayashi
   Proceedings of 13th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC), vol.111, pp.10:1-10:20, 2018.
   Presented at TQC2018 (Talk).

   Quantum multiple-unicast network is a network in which multiple sender-receiver pairs communicate respective quantum states at the same time. This paper concretely constructs a quantum network code for the quantum multiple-unicast network. The proposed code is constructed only by the coding operation of the senders and the receivers but without manipulation of the node operations.

3. Quantum State Transmission over Partially Corrupted Quantum Information Network
   by Masahito Hayashi and Seunghoan Song
   Physical Review Research, 2, 033079, 2020.

   Though paper [4] studied a concrete construction of secure quantum network codes, the optimality has not been proved. This paper derives a lower bound of the optimal transmission rate for partially corrupted quantum networks, under the assumption that the positions of corrupted edges are known to the sender and the receiver. Consequently, the quantum network code in [4] is shown to be almost optimal.

1. Sphere Packing Bound and Gilbert-Varshamov Bound for b-Symbol Read Channels
   by Seunghoan Song and Toru Fujiwara
   IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol.e101-a, pp.1915-1924, 2018.

   b-symbol read channel is a channel model in which b consecutive symbols are read at once. This channel model is motivated by a limitation of high-density storage media, namely, that reading devices fail to isolate each symbol recorded at high density. As special cases, it includes the symbol-pair read channel (b = 2) and the ordinary channel (b = 1). In this paper, we derive the sphere packing bound, the Gilbert-Varshamov bound, and the asymptotic Gilbert-Varshamov bound for b-symbol read channels with b ≥ 1.