ファイル更新日：2007年11月22日

研究情報

■第6回名古屋国際数学コンファレンス■

●Representation Theory of Algebraic Groups and Quantum Groups 06

Date

June 12–17, 2006

Place

Noyori Conference Hall, Nagoya University

Speakers

H. H. Andersen (Aarhus), T. Arakawa (Nara), S. Ariki (Kyoto), J. Du (Sydney), M. Geck (Aberdeen), V. Ginzburg (Chicago), J. C. Jantzen (Aarhus), S.-J. Kang (Seoul), M. Kashiwara (Kyoto), S. Kato (Tokyo), G. I. Lehrer (Sydney), G. Lusztig (Boston), I. Mirkovic (Boston), H. Miyachi (Nagoya), H. Nakajima (Kyoto), T. Nakashima (Tokyo), R. Rouquier (Leeds), D. Sagaki (Tsukuba), Y. Saito (Tokyo), O. Schiffmann (Paris), T. Suzuki (Kyoto), T. Tanisaki (Osaka), J. Xiao (Beijing)

Organizing Committee

T. Shoji (Nagoya, Chair), A. Gyoja (Nagoya), H. Nakajima (Kyoto), K. Shinoda (Sophia), T. Tanisaki (Osaka City)

Directions

• Directions to Nagoya University [English]
• Directions to Nagoya University [Japanese]

Official Page

The 6th International Conference
Representation Theory of Algebraic Groups and Quantum Groups 06
(Speakers / Preprint Buffer / Fuding / Registration / Lodging and Travel / Organizing Committee / Banquet / Conference Poster / List of Participants / Abstracts / Program and etc.)

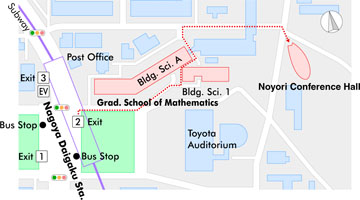
●Route Map from Nagoya Daigaku Station to Noyori Conference Hall